Limits

Limits

Delta Epsilon Definition

Let $I$ be an open interval containing $a$, and let $f$ be a function defined on $I$, except possibly at $a$. The limit of $f(x)$ as $x$ approaches $a$ is $L$, donoted as

\[\lim_{x \to a} f(x) = L,\]

means that given any $\epsilon > 0$, there exists $\delta > 0$ such that for all $x \neq a$, if $|x - a| < \delta$, then $|f(x) - L| < \epsilon.$

This means that when we pick any value of $\epsilon > 0$ first to make a range of $y$ values around $L$, that is, $|y - L| < \epsilon$, if we can always find a value of $\delta > 0$ around $a$ such that when $|x - a| < \delta$, $|f(x) - L| < \epsilon$, then the limit as $x$ approaches $a$ is $L$.

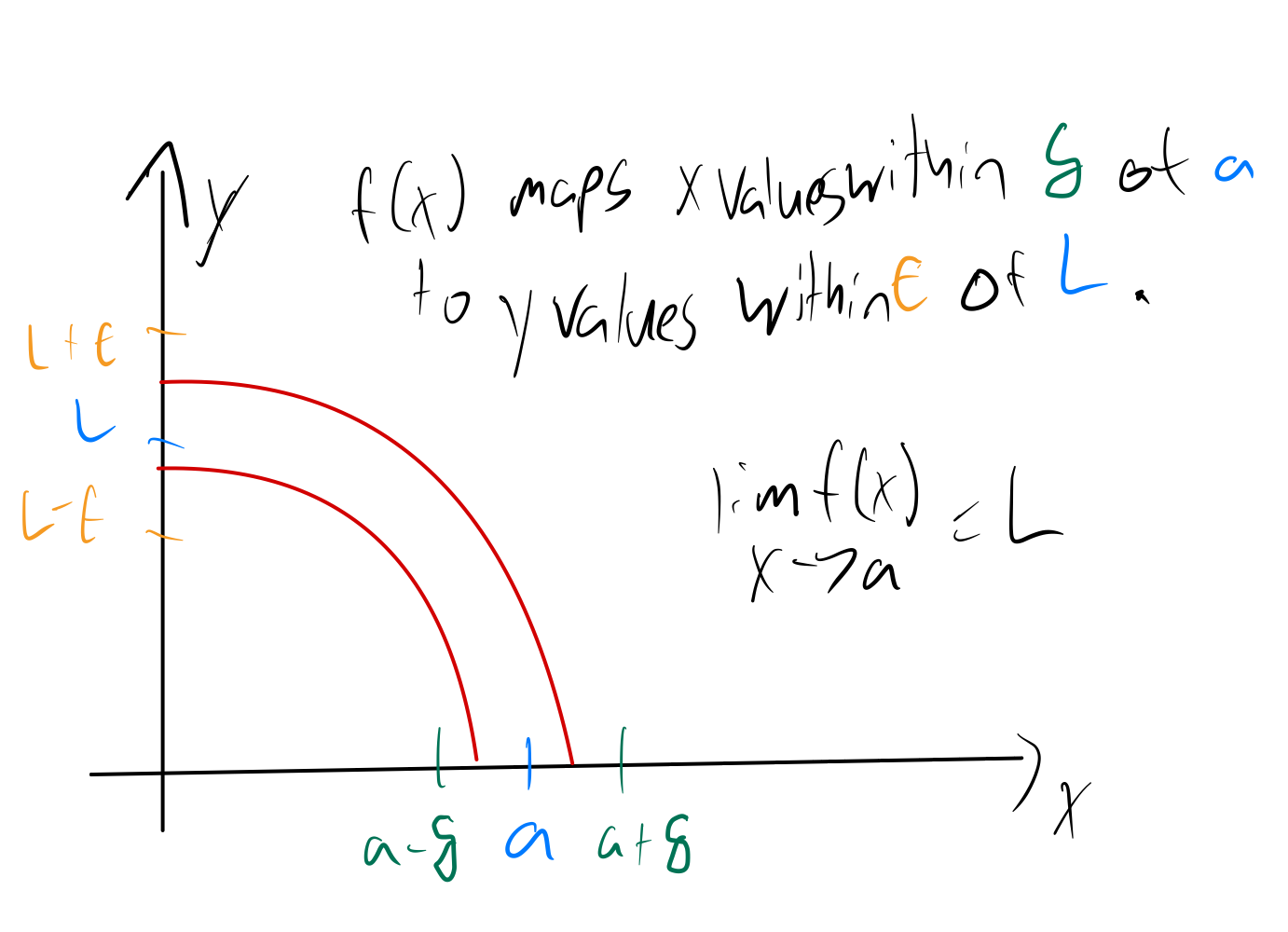
Example

Prove

\[\lim_{x \to 1} \frac{3x(x-1)}{x-1} = 3.\]

We need to show that given $\epsilon > 0$, there exists $\delta > 0$ such that

\[0 < |x - 1| < \delta \implies \left | \frac{3x(x-1)}{x-1} - 3 \right | < \epsilon\]

Basically, we need to find $\delta$ as a function of $\epsilon$ here to show that no matter what the value of $\epsilon$ is, we can find a satisfactory $\delta$.

We can do this with some algebraic manipulation:

\[\left | \frac{3x(x-1)}{x-1} - 3 \right | < \epsilon \iff \left |3x - 3 \right | < \epsilon \iff |x -1| < \frac{\epsilon}{3}\]

Now we’ve shown that as long as $|\delta| < \frac{\epsilon}{3}$, then $|f(1 - \delta) - 3| < \epsilon$.

Tricks

Factoring a root out of a numerator

Say we have:

\[\lim_{n \to \infty} \frac{n + 1}{\sqrt{(n + 1)(2n+1)}}\]

Since $n$ is going to infinity it is positive and for positive $n$, $n + 1 = \sqrt{(n+1)^2)$ we can factor out a root to simplify:

\[\lim_{n \to \infty} \frac{\sqrt{(n + 1)^2}}{\sqrt{(n + 1)(2n+1)}} = \lim_{n \to \infty} \sqrt{\frac{(n + 1)^2}{(n + 1)(2n+1)}} = \lim_{n \to \infty} \sqrt{\frac{n+1}{2n+1}}\]

From there we can move the limit inside the radical:

\[\sqrt{\lim_{n \to \infty} \frac{n + 1}{2n + 1}} = \sqrt{\frac{1}{2}} = \frac{\sqrt{2}}{2}\]