Limits and Continuity of Complex Functions
Limits of Complex Functions
See first the Limits notes for two dimensional functions.
Delta Epsilon Definition
Let $S$ be an open set containing $a$, and let $f$ be a function defined on $S$, except possibly at $a$. The limit of $f(z)$ as $z$ approaches $a$ is $L$, donoted as
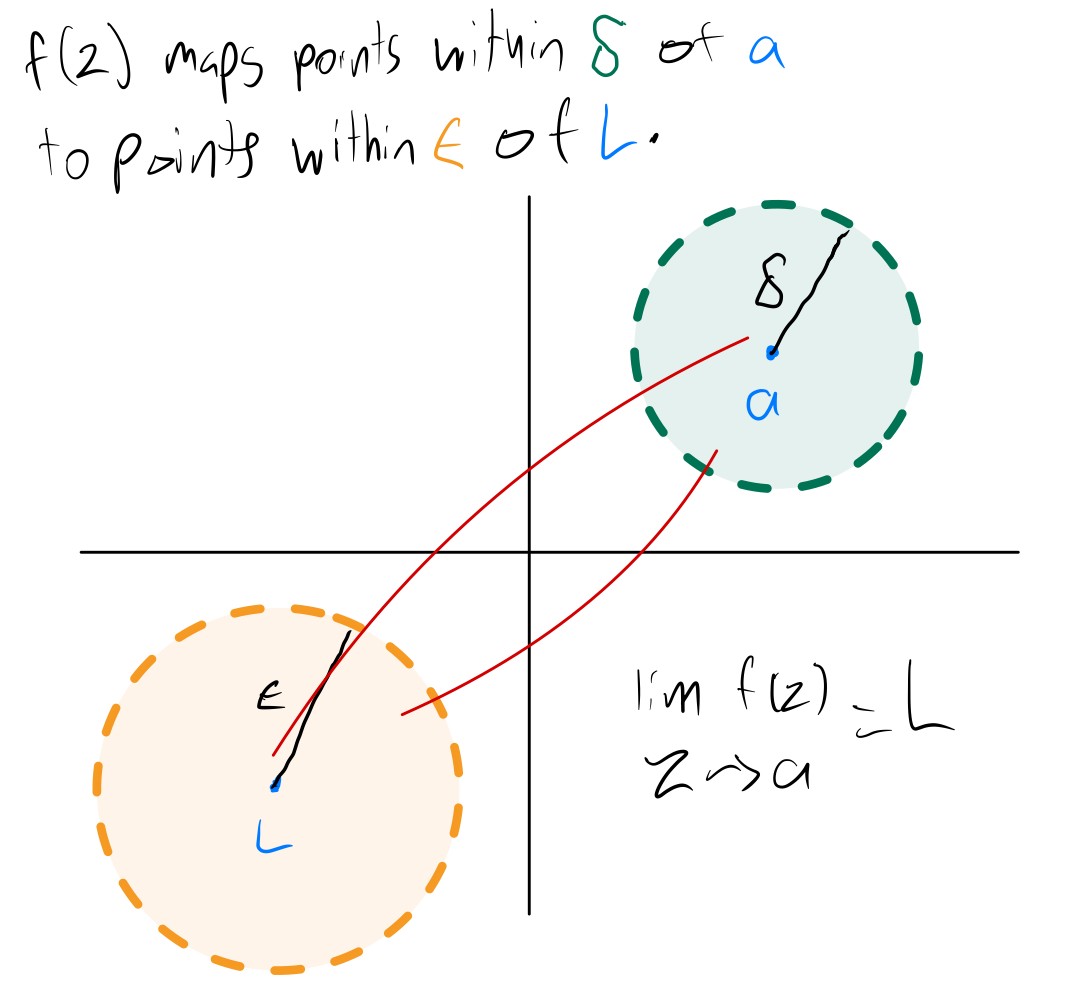
\[\lim_{z \to a} f(z) = L,\]means that given any $\epsilon > 0$, there exists $\delta > 0$ such that for all $z \in S, z \neq a$, if $|z - a| < \delta$, then $|f(z) - L| < \epsilon.$
This means that when we pick any value of $\epsilon > 0$ first to make an open disc of $w$ values around $L$, that is, $|w - L| < \epsilon$, if we can always find a value of $\delta > 0$ such that when $|z - a| < \delta$, $|f(z) - L| < \epsilon$, then the limit of $f(z)$ as $z$ approaches $a$ is $L$.
This is similar to limits of two dimension functions, except that instead of having open intervals on the $x$ and $y$ axis, respectively, around $a$ and $L$, we have open discs in the $z$ and $w$ planes, respectively, around $a$ and $L$.
Whereas for limits on the 2d plane to exist, we need to get the same limit approaching from the left or right of $a$, for limits on the complex plane to exist, we need to get the same limit approaching $a$ from any direction.
Continuity
A complex function $f$ is said to be continuous at $z = z_0$ if
\[\lim_{z \to z_0} f(z) = f(z_0)\]The function is said to be continuous on an open set if it is continuous at each point in the set. This definition imposes three conditions of the function $f$:
-
$f$ must be defined at $z_0$;
-
the limit of $f$ as $z \to z_0$ must exist;
-
the numbers in 1. and 2. must be identical.
Continuous functions can be added, subtracted, multiplied, and divided, and their results will still be continuous.
A discontinuity in a function $f$ at $z_0$ is said to be a removable discontinuity if we can assign a value to the function $f$ at $z_0$ that makes the function continuous.
Branches, Branch Points and Branch Cuts
A multi-valued function such as $\arg{z}$ can be made single valued by restricting its range. For example, if we restrict the range of $\arg{z}$ to be $0 \le \arg{z} < 2 \pi$, then it is single valued. $\arg{z}$ restricted in this manner will be discontinuous at $z = 0$ and along the positive real axis.
We could similarly restrict the range to any other interval $[\phi, \phi + 2 \pi)$ and call this fuction $\arg_{\phi}{z}$ and it will be discontinuous at $z = 0$ and along the half-line that forms the angle $\phi$ with the positive real axis.
This restricted range version of $\arg{z}$ is said to be a branch of $\arg{z}$. The half-line along which it is discontinuous is called the branch cut of the branch, and the point $z = 0$ at which all branch cuts meet is called the branch point of the multi-valued function $\arg{z}$.