Contour Integrals
Contour Integrals
A contour integral is essentially a line integral in the complex plane.
Given a smooth curve $C$ in a domain $D$ and $f(z) = u(x,y) + v(x,y)i$ a contiuous function defined along $C$, we say that
\[\int_{C} f(z) dz = \int_C (u+vi)(dx + dyi) = \int_C u dx - vdy + i \int_C vdx + u dy.\]We can parameterize $C$ such that
\[C : z = z(t) = x(t) + y(t)i, \quad \alpha \le t \le \beta\]Then we have
\[\int_C f(z) dz = \int_\alpha^\beta f[z(t)]z'(t) dt\]One trick we can use is that when the modulus of a function is constant, we can use the argument of $z$ as a parameter by writing $C: z = e^{\theta i}, \arg{\alpha} \le \theta \le \arg{\beta}$
When the path of integration in a contour integral is a closed curve, we place a circle on the integral sign
\[\oint_C f(z) dz.\]You can add an arrow to the circle to indicate clockwise vs counterclockwise direction, but that’s not supported in MathJax so I don’t have it here!
Some additional properties:
\[\text{Re} \int_C f(z) dz = \int_C \text{Re}[f(z)dz];\] \[\text{Im} \int_C f(z) dz = \int_C \text{Im}[f(z)dz];\] \[\left | \int_C f(z) dz \right | \le \int_C |f(z)||dz| \le ML\]where $M$ is the maximum value of $|f(z)|$ for $z$ on $C$, and $L$ is the length of $C$.
Here’s an example problem: evaluate $\oint_C e^z dz$ where $C$ is the closed (traingular) path from $0$ to $1$ ($C_1$) to $1 + i$ ($C_2$) back to $0$ ($C_3$):
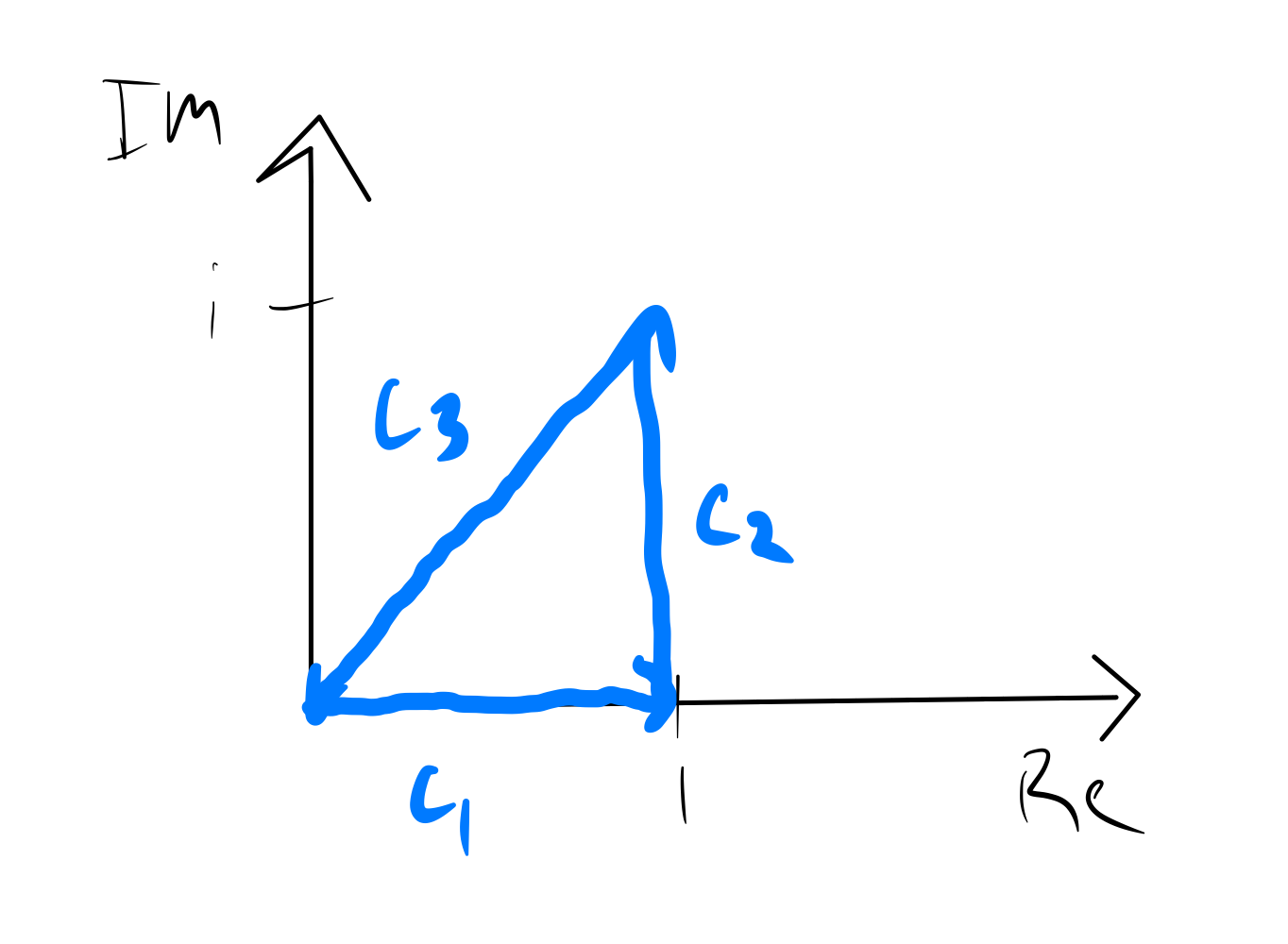
where
\[C_1: y = 0, 0 \le x \le 1;\] \[C_2: x = 1, 0 \le y \le 1;\] \[C_3: x = t, y = t, 1 \ge t \ge 0;\]Thus,
\[\oint_C e^z dz = \int_0^1 e^x dx + \int_0^1 e^{1+yi}idy + \int_1^0 e^{t+ti} (dt +dt~i)\] \[= \left \{ e^x \right \}^1_0 + \left \{ e^{1+yi} \right \}^1_0 + \left \{ e^{(1+i)t} \right \}^0_1\] \[= (e - 1) + (e^{1+i} -e) + (1 - e^{1 +i}) = 0.\]