Cauchy-Goursat Theorem

Cauchy-Goursat Theorem

First, a less general theorem that can be shown using Green’s theorem:

If the derivative $f^{\prime }$ of a complex function $f$ is continuous in a domain containing a simple, closed, piecewise smooth curve $C$ and its interior, then

$${\oint }_{c}f(z)dz=0.$$

The Cauchy-Goursat Theorem is more general and doesn’t require continuity of $f^{\prime }$:

If $f$ is analytic inside and on a closed, piecewise smooth curve $C$, then

$${\oint }_{c}f(z)dz=0.$$

Note that $f$ has to be analytic both on and inside the piecewise smooth curve $C$. This means that if $C$ encloses a singularity, then Cauchy-Goursat can’t be applied directly.

In these cases we can apply an extension of Cauchy-Goursat:

Let $C$ be a simple, closed piecewise smooth curve, and $C_1$, $C_2$, $\dots$, $C_n$ be disjoint, simple, closed piecewise smooth curves in the interior of $C$. If $f$ is analytic at all points that are both inside or on $C$, and outside or on each $C_j$, then

$${\oint }_{c}f(z)dz=\sum _{j=1}^n{\oint }_{C_j}f(z)dz.$$

This arms us with a method to find the following contour integral:

$${\oint }_C\frac{1}{z^2-1},C:|z|=4.$$

Since $f(z)=\frac{1}{z^2-1}$ has singularities at $-1$ and $1$ that are completely encircled by $C$, it’s not obvious whether or not $f$ has an antiderivative along $C$. However, we can apply the theorem above by encircling the singularities:

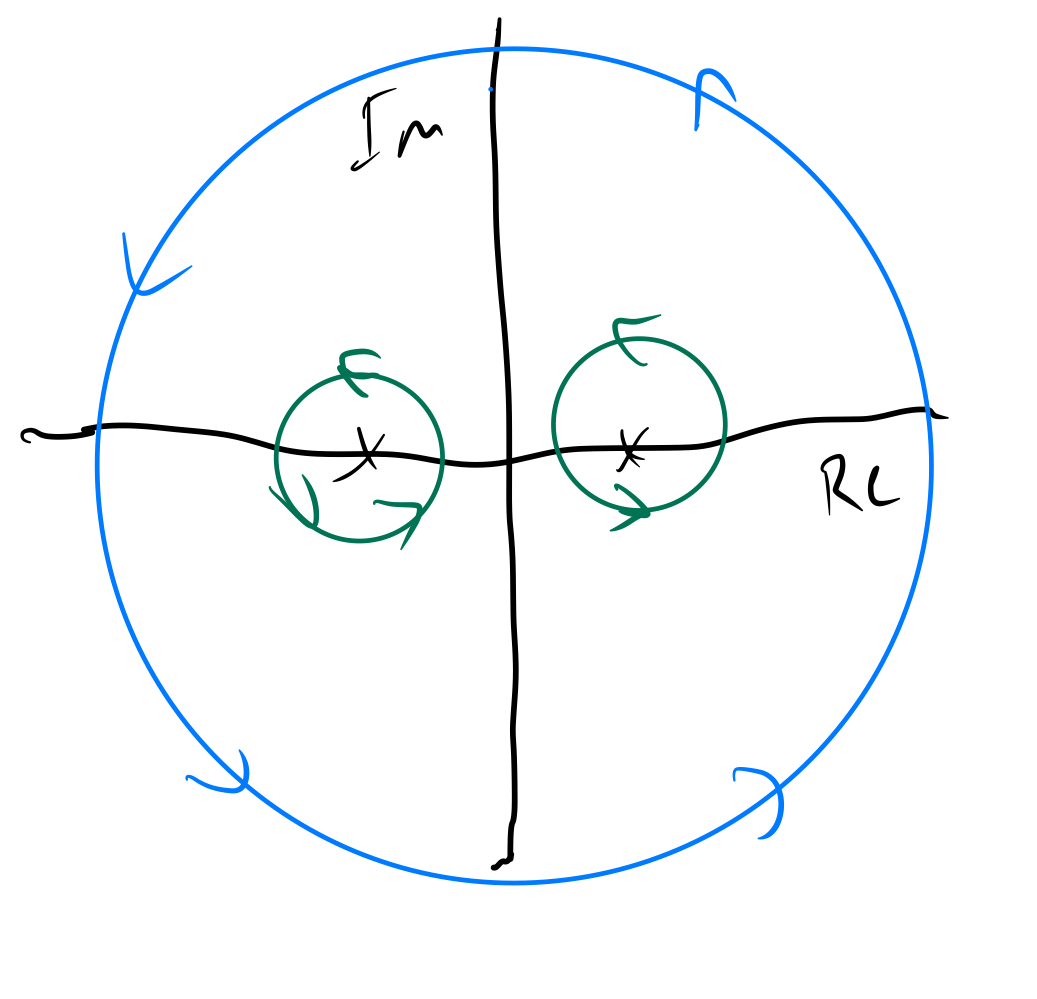
Now we can find our contour integral by evaluating the contour integrals on paths around our singularities, as these paths are analytic everywhere outside them but inside $C$.

A useful theorem to proceed from here is the following:

If $C$ is a simple, closed, piecewise smooth curve and $z_0$ is interior to $C$, then:

$${\oint }_C\frac{1}{z-z_0}dz=2\pi i.$$

Now, via partial fraction decomposition we have

$${\oint }_C\frac{1}{z^2-1}=\frac{1}{2}{\oint }_C\frac{1}{z-1}-\frac{1}{z+1}dz=\frac{1}{2}({\oint }_C\frac{1}{z-1}dz-{\oint }_C\frac{1}{z+1}dz)=\frac{1}{2}(2\pi i-2\pi i)=0.$$

The following theorems illustrate the nice properties of simply connected domains, where we don’t have to deal with singularities or holes:

When $f$ is analytic in a simply-connected domain $D$, the contour integral of $f$ around every closed, piecewise smooth curve in $D$ vanishes.

When $f$ is analytic in a simply-connected domain $D$, the contour integral of $f$ is independent of path in $D$.

When $f$ is analytic in a simply-connected domain $D$, it has an antiderivative therein.