Geometric Problems
Geometric Problems
jmh: my notes
Problems Relating to the Tangent Lines to an Unknown Family of Curves
This lesson starts by discussing a few problems for finding families of curves with some property relating to tangets to points on the curve. Differential equations arise here because the slope of the tangent line in these cases is $y’$. Generally, we’ll know we want some family of functions who’s derivative has some proprety, and we use that property to find the family of functions.
Background
We need some stuff from algebra, Calculus 3 and linear algebra here.
I’ll list some of the useful formulas.
Midpoint Formula The mid-point formula for two points $(x_1, y_1)$ and $(x_2,y_2)$ is:
\[(\frac{x_1+x_2}{2},\frac{y_1 + y_2}{2})\]Projection
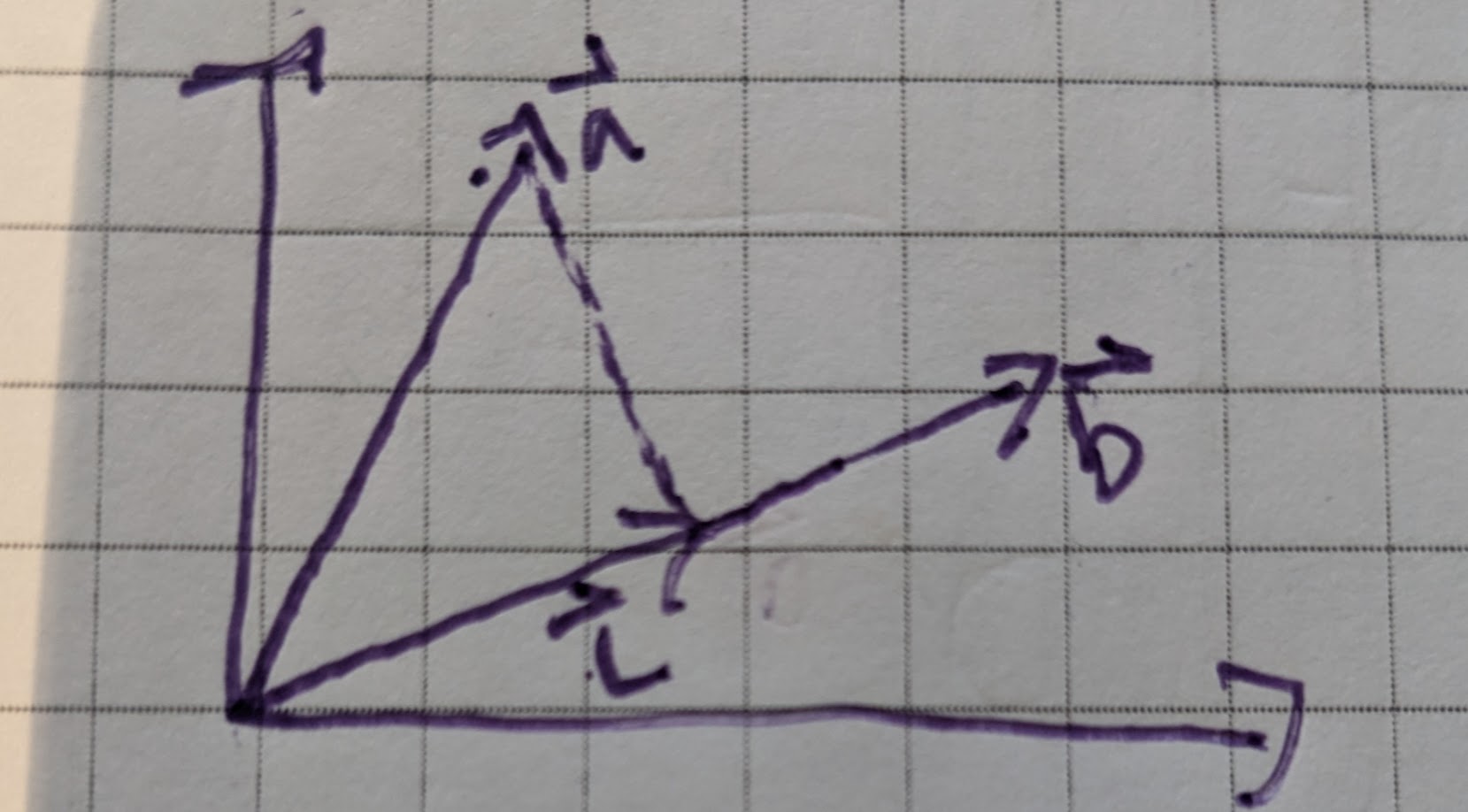
A projection of $\vec{a}$ onto $\vec{b}$ is a new vector $\vec{c}$ in the direction of $\vec{b}$ representing the portion of $\vec{a}$ that’s in the direction of $\vec{b}$. Geometrically, we can find $\vec{b}$ by drawing a line perpindicular to $\vec{b}$ passing through the end of $\vec{a}$. Where this line intersects $\vec{b}$ will be the end of $\vec{c}$
Tangent Line and Normal Line The tangent line (or simply tangent) to a plane curve at a given point is the straight line that “just touches” the curve at that point. Its slope is $y’$.
The normal line is the line perpindicular to the tangent line at the point of tangency. Its slope is $-\frac{1}{y’}$.
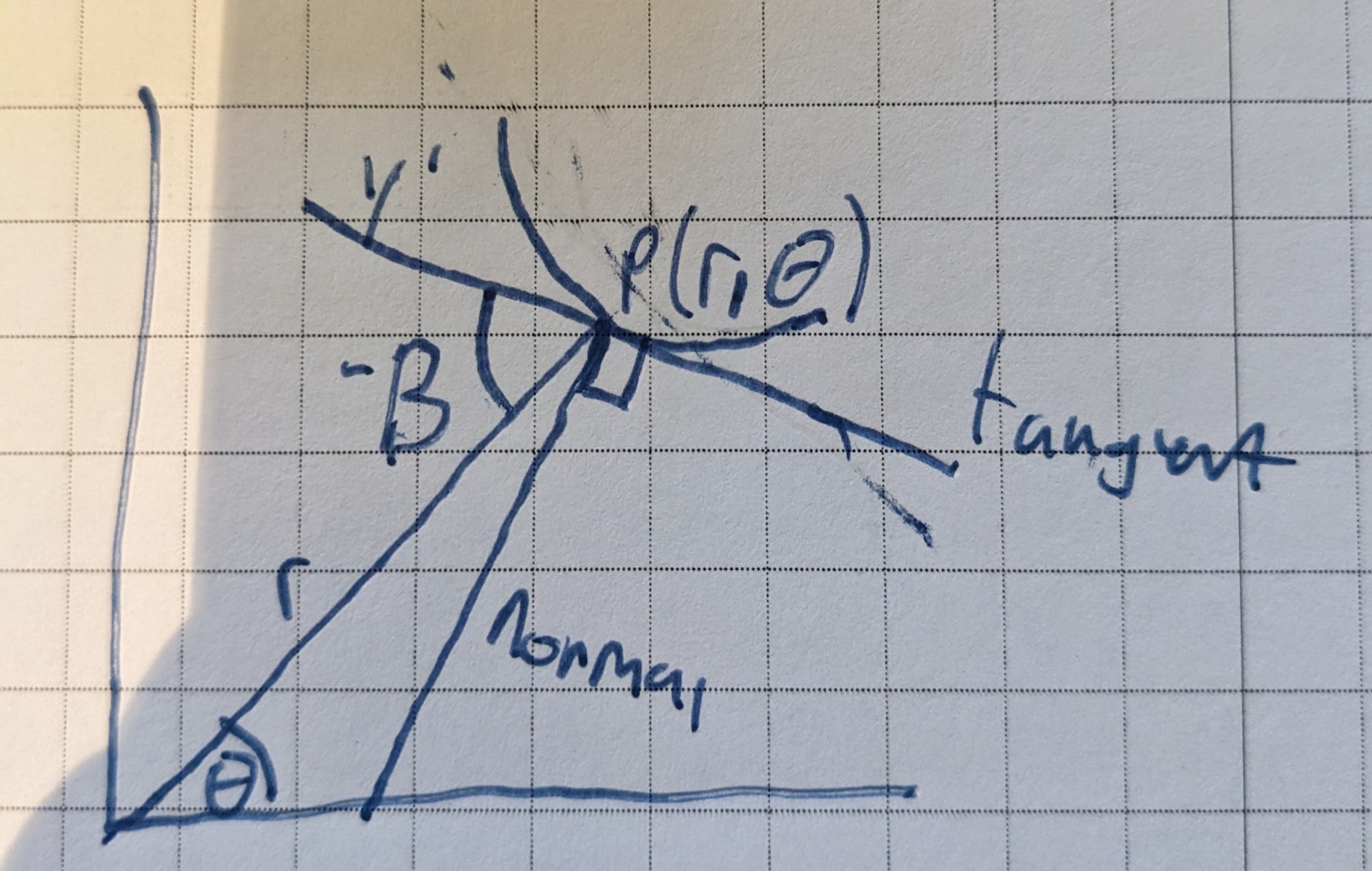
Subtangent The subtangent is the length of the projection of the tangent line on the $x$-axis, i.e., the distance from the $x$-intercept of the tangent line and $x$. Its value is $|\frac{y}{y’}|$.
Subnormal The subnormal is the length of the projection of the normal line on the $x$-axis, i.e., the distance from the $x$-intercept of the normal line and $x$. Its value is $|yy’|$.
Radius Vector A radius vector is a vector from the origin to a point on a curve. It is $r$ in the picture above.
The angle $\beta$ between the radius vector and the tangent line at point P is given by:
\[\tan{\beta} = r\frac{d0}{dr}\]Abscissa The $x$ value of a point. Aka the straight line distance from the $y$-axis to the point.
Ordinate The $y$ value of a point. Aka the straight line distance from the $x$-axis to the point.
Method of Solution
The problems are started in the form “find the family of curves” meeting some requirements related to tangent lines of the family of curves. Since we have to find the family, not just a family, we must show that the family we find meets the requirements (sufficient) and than any curve meeting the requirements will be in the family we find (necessary).
Proof of Necessesity
The tangent line in the problem will have a slope given by $y’$ - the derivative of the curve. We can use that, along with the other requirements in the problem, to setup and solve a differental equation relating $y’$ to $y$ and $x$. This gives an equation that defines the function $y(x)$, and shows that any family of curves that meet the requirements of the problem will satisfy that equation.
Proof of Sufficiency
To show that the family of curves found will satisfy our requirements, we can pick a point $P(x_0, y_0)$ on the curve, then find the derivative of the function at that point (first find/isolate $y_0$ at that point, then differentiate both sides with respect to $x$) which gives the slope of the tangent line at the point. We can then reason further to show that the tangent line meets whatever requirements the problem set forth to show that family of curves satisfies the requirements of the problem.